AlphaZero Homebrew

Homebrew your own AlphaZero

Let’s have a look at the AlphaZero algorithm, implement it for the game of TicTacToe, and inspect its performance. All the code can be found in this repository.

“The game Tic Tac Toe being played by steampunk computers, digital art”

Overview

Issue: Some problems (such as the game of Go) have very wide decision trees. For a 19x19 board, there are 361 possibilities for the first move. To map all of the first two moves, there are 361*350=129960 possibilities. First three? Over 46 million. Due to the severity of this increase, previous approaches (such as alpha-beta pruning) become infeasible.

Solution: The AlphaZero (AZ) algorithm doesn’t perform a full tree search, but rather uses a probabilistic search algorithm (Monte-Carlo tree search: MCTS) to explore only those sections of the tree that are deemed most promising. MCTS is combined with a neural network in the following way:

The current board-state is fed through a network that is trained to indicate promising moves to make. This provides a prior distribution over moves to kickstart the MCTS.

• A hypothetical move is selected and the algorithm interacts with a simulator to update the board state. At this point, one of following possibilities exist:

  • This board state has been visited before in this MCTS-session.
    • In this case we select another action and progress the board state until we reach a state that has not been visited yet.
  • This board state has not been visited before in this MCTS-session yet.
    • If the game has ended, we check whether its a win, draw, or loss. This is translated into a value (1, 0, -1 respectively).
    • If the game hasn’t ended, we ask a neural net to provide an estimate of how ‘good’ this board state is; it’ll return a value between 1 and -1. Alternatively, the game may be played until the end in simulation to provide a value estimate (“rollout”).

Whichever it is, we now have a value estimate of how ‘good’ the path we explored is. This is pushed back up the tree and associated with the moves that led us here.

Monte-Carlo Tree Search source

Code & Classes

• neural_nets.py: Contains the PyTorch models used by the MCTS algorithm.

  • Mainly for testing purposes, the value ($v = f_\theta(s)$) and policy ($p=f_\theta(s)$) networks are here different models. They take in the current board state $s$ and they provide:
  \[\begin{align} p_a &= Pr(a|s) \newline v &= \mathbb{E}[z|s] \end{align}\]

  with $z$ being the game outcome, $v$ an estimator of the expected game outcome $z$, and $p_a$ a vector of move probabilities.

  • The value-net is trained using a MSE loss computed using its value estimate $v$ and actual game outcome $z$. Meanwhile, we use a Cross-Entropy loss for the policy net between the generated prior move-probabilities $p_a$ and the distribution over moves generated by MCTS $\pi$:
  \[\begin{align} l_p &= -\pi \log p_a \newline l_v &= (z - v)^2 \end{align}\]

• mcts.py: Contains an implementation of the MCTS algorithm. However, how exactly does MCTS select actions?

  • A UCT (Upper Confidence bound for Trees) is computed as follows:
  \[\begin{align} UCT(s,a) = c p_a \frac{\sqrt{\sum_A N(s,A))}}{1 + N(s,a)} \end{align}\]

  where $p_a$ are the prior move probabilities provided by the network and $N$ the amount of times we’ve taken a certain action $a$ (in the numerator we sum over all potential actions $A$). The method does some exploration-exploitation balancing by favouring high $p_a$ (exploitation) while decreasing repeated visits as $N(s,a)$ increases (exploration). The $c$ is a constant that shifts this balance.

• TTT_env.py: Contains the TicTacToe environment that MCTS can call upon to check the game state.

• self_play.py: Here we combine all previous pieces and enables the AZ ‘loop’:

  We initialize the model and evaluate its performance (here, simply against random play).

  then, while current iteration $<$ total iterations:

  1. The model plays against itself by iteratively choosing actions via MCTS.

  2. We use the observed game-states and the associated $\pi$ and $z$ to train the network(s).

  3. Re-evaluate the model’s performance.

  4. current iteration ++

Let’s play

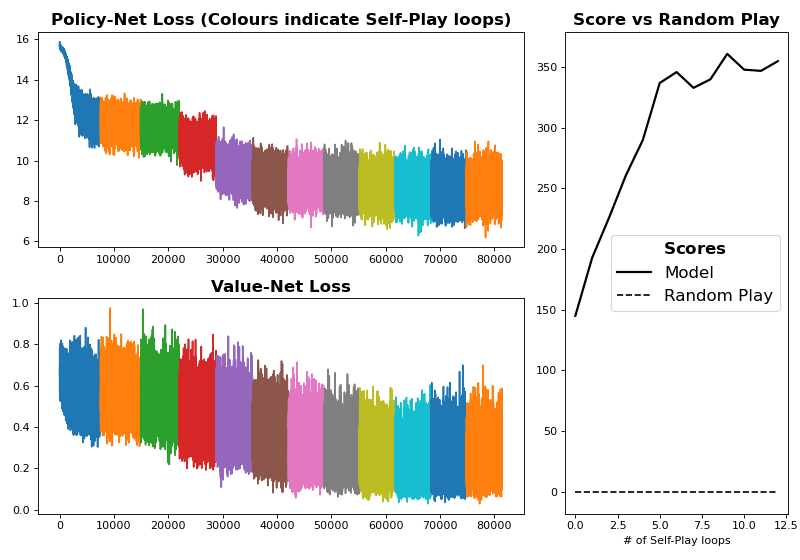
Here I’ve ran the model for 12 iterations with 1000 games per iteration and an MCTS depth of 15. I’ve segmented the loss colour-wise to show the progression from one version of the model to the next. The ‘score’ (wins minus losses) of AZ against random-play more than doubles in only a couple of iterations. It’s noteworthy that the model starts off much better than random play (at ~150 instead of 0). This is because TicTacToe is quite a shallow game, and thus even a very shallow MCTS already boosts our performance by quite a bit.

Before inspecting AZ further, it might be useful to briefly visualize the MCTS results.

MCTS in action

Left, a board is plotted. MCTS is the ‘x’-player. In this position, there are 5 possible moves with one obvious best option. Here MCTS ran for 20 iterations and the bar-plot shows the amount of times we selected each move. By running these visit counts through a soft-max operation ($\frac{e^{N_a}}{\sum_A e^{N_A}}$) we get $\pi$: a probability distribution over moves, which I laid over the board on the left.

Value-net in action

To get some insight into whether the training worked, let’s run the board evaluation on some examples:

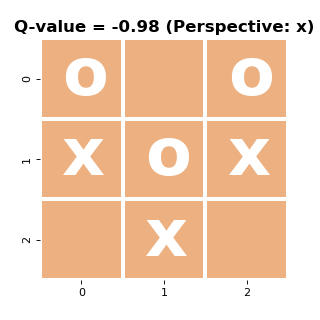
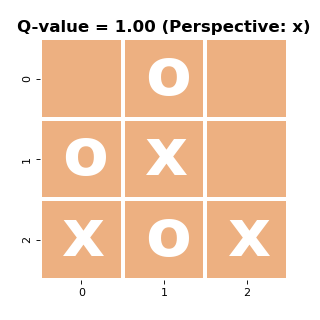
Again from the ‘x’-perspective, the left board is terrible and is a guaranteed loss. Meanwhile, the right board is great as we can guarantee ourselves a win with multiple moves. Above the board I’ve included the value estimates of the network when fed these game-states and we can see that (at least for this tiny sample) the network produces useful results that can aid the tree search.

Policy-net in action

Finally, let’s see how the priors on the policies are shaped across iterations. Here, for the initial 6 iterations I’ll feed a board to the policy-net and overlay the output $p_a$ on the board.

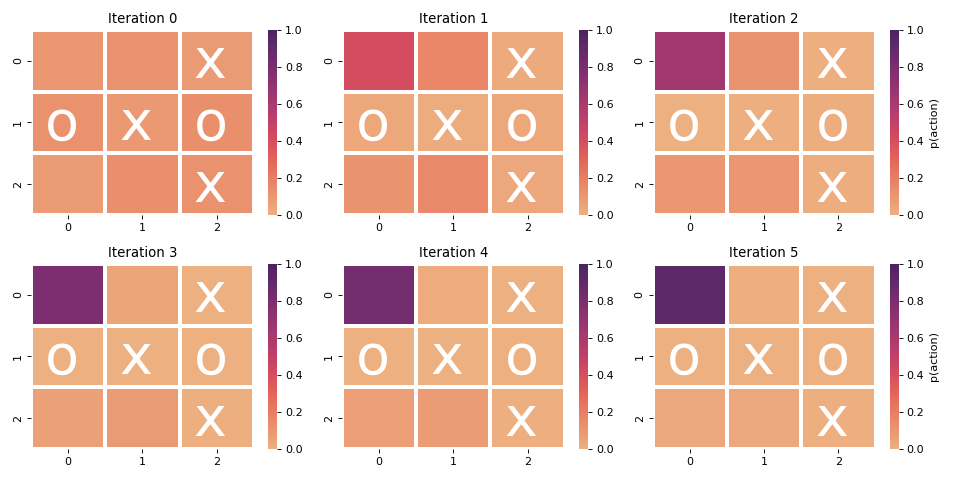
This is an easy one, with moves on (0,0) and (2,0) guaranteeing a victory. Ideally, the network doesn’t put all of its weight into one of them, but perhaps because the game finishes once the action is taken, the model cannot be punished for choosing move (0,0).

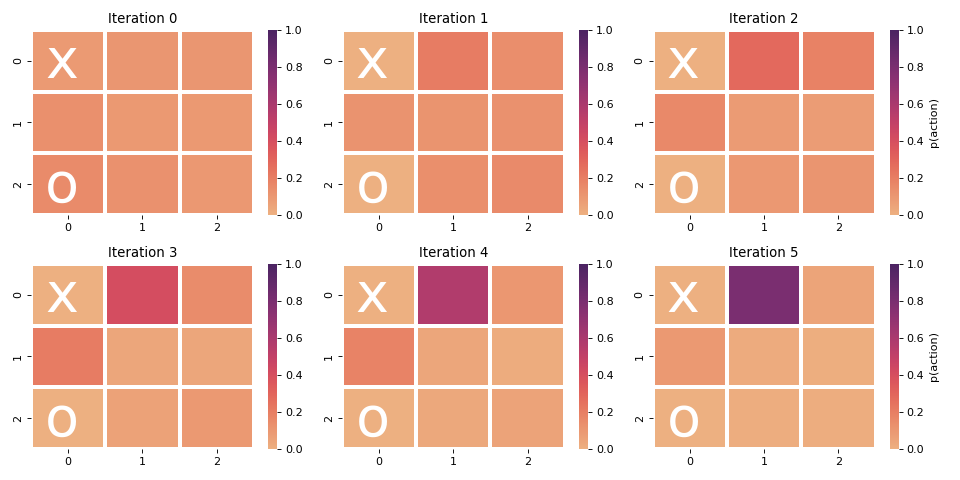
This is quite a nice result. It’s still early in the game, but we can guarantee a win here by playing (0,1) into (1,1), which the network seems to suggest. However, this is again not the only move with such a high value and it would be nice to produce distribution with greater entropy.

Some final notes

• Play around with the exploration-explotation balance in the UCT scoring. MCTS being more entropic will also make policy net more entropic.

• Data augmentation

• To prevent potential distributional drift, use a more systematic way to select self-play opponents.

• Dirichlet noise.

Twitter  facebook  Email